Introduction:
An equation is a mathematical statement that asserts the equality of two expressions. [1] Equations consist of the expressions that to be equal on opposite sides of an equal sign, as in
An equation is the combination of two expressions separated by an equal sign. In the equation the both sides of the equal sign has the same value.
For example,
2 + 18 = 4 * 5
Transcendental Equations
If f(x) is a polynomial in x, then f(x) = 0 is an algebraic equation.
Example; x7 + 5x - 2 = 0.
If f(x) contains algebraic and non algebraic functions namely exponential, logarithmic, trigonometric and inverse trigonometric functions then f(x) = 0 is called transcendental equation.
Example; x + log x + sin x=0.
Transcendental equations may have no root, exactly one root or more than one root.
Algebraic Equations:
Fundamental theorem on Algebra.
Every algebraic equation of degree n ≥ 1 has a root real or complex.
An equation is a mathematical statement that asserts the equality of two expressions. [1] Equations consist of the expressions that to be equal on opposite sides of an equal sign, as in
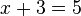
An equation is the combination of two expressions separated by an equal sign. In the equation the both sides of the equal sign has the same value.
For example,
2 + 18 = 4 * 5
Types of Equations:
Fundamentals and types of Equations are :Transcendental Equations
If f(x) is a polynomial in x, then f(x) = 0 is an algebraic equation.
Example; x7 + 5x - 2 = 0.
If f(x) contains algebraic and non algebraic functions namely exponential, logarithmic, trigonometric and inverse trigonometric functions then f(x) = 0 is called transcendental equation.
Example; x + log x + sin x=0.
Transcendental equations may have no root, exactly one root or more than one root.
Algebraic Equations:
Fundamental theorem on Algebra.
Every algebraic equation of degree n ≥ 1 has a root real or complex.

No comments:
Post a Comment